최대우도추정 (Maximum likelihood estimation)

최대우도추정 (Maximum likelihood estimation)

확률 및 통게 2020. 11. 2. 18:28
가능도 (Likelihood)와 최대우도추정법이 무엇인지 직관적으로 이해하기 위한 정리이다.

이 두가지 개념을 설명하기에 앞서 확률에 대해 간단히 언급해보겠다.

확률

주사위를 예를 들어보자. 주사위를 던져서 나올 수 있는 숫자의 확률은 1/6 으로 모두 같다.

동전 던지기를 100번 시행 해서 앞면이 56번 나왔다고 가정하자. 반복적인 동전던지기는 이항분포(bionomial distribution)을 따른다.

이항 분포 식을 참고해서 동전 10번 던져서 앞면은 0~10번 나올 수 있으며 각각의 확률은 계산해 보면 각각 0.001, 0.01, 0.044, 0.117, 0.205, 0.246, 0.205, 0.117, 0.044, 0.01, 0.001 이다. 두 경우 모두 일어날 수 있는 사건이 6개, 11개로 정해져 있으며 각각에 대한 확률을 구할 수 있고 확률의 합은 1이 된다.

연속 사건의 확률

특정사건의 확률을 생각해보자. 1~6사이의 숫자 중 랜덤으로 아무거나 뽑는다고 생각해보자. 주사위와는 다른 개념이다. 주사위는 1,2,3,4,5,6 이라는 경우가 있지만 위와 같은 경우는 1.2,1.3등 무한한 많은 숫자가 있고 이때 정확히 4라는 숫자를 뽑을 확률은 $\frac{1}{\infty} = 0$

$\frac{1}{\infty} = 0$

$\frac{1}{\infty} = 0$

$\frac{1}{\infty} = 0$

$\frac{1}{\infty} = 0$

확률 밀도 함수 f(x)는 어떤 확률 변수의 크기를 나타내는 값이다. a와 b사이의 확률을 구하는 것은 확률밀도함수 그래프의 넓이를 구하는 것이다.

1~6사이에서 2~4사이의 숫자가 뽑힐 확률밀도함수 그래프

위 그림은 예시이고 적분을 통해 넓이를 구하고 확률을 구한다.

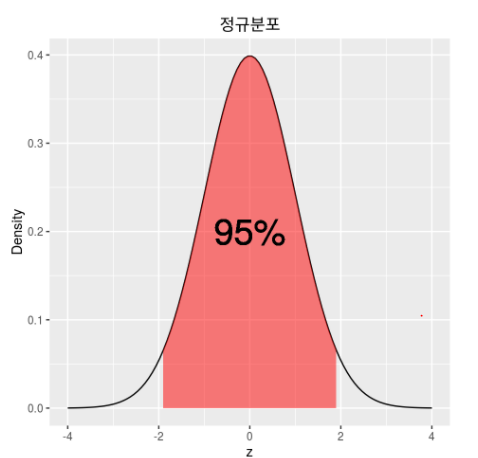
위 그림은 가장 흔히 쓰이는 평균 0, 분산 1인 표준정규분포(Standard normal distribution)를 나타내고 있다. 표준정규분포의 PDF는

표준정규밀도함수

로 표현되며

그림에서 보듯이 $z$ 가 -1.96~1.96에 안에 있을 확률이 95%임을 알 수 있다.

특정 사건이 일어날 가능성을 비교할 수는 없을까??

연속사건에서는 특정 사건이 일어날 확률이 전부 0으로 계산되기 때문에 사건들이 일어날 가능성을 비교하는 것이 불가능하고, 가능도라는 개념을 적용해야 한다. 직관적으로 가능도를 생각해보면 위의 그래프들에서 y값을 가능도라고 생각하면 된다. 즉 y값이 높아질수록 해당 사건이 일어날 가능성이 높은 사건이다. 주사위나 동전을 던지는 경우는 확률=가능도가 된다.

한편 연속사건인 경우 (정규분포) PDF의 값이 바로 y가 되며 위 그림에서 0에 해당되는 PDF값(Y값)이 0.4로 1에 해당되는 PDF값(Y값) 0.24보다 높아 0 근처의 숫자가 나올 가능성이 1 근처의 숫자가 나올 가능성보다 높다고 할 수 있고 이를 Likelihood와 같게 생각하면 된다.

가능도의 직관적인 정의 : 확률분포함수의 y값

셀 수 있는 사건: 가능도 = 확률

연속 사건: 가능도 $\neq$ 확률, 가능도 = PDF값

이미 주어진 표본 $x$ 들에 비추어 봤을 때 모집단의 모수 $θ$ 에 대한 추정이 그럴듯한 정도를 Likelihood(우도) 라고 한다.

우도 $L (θ$ | $x)$ 는 $θ$ 가 전제되었을 때 표본 $x$ 가 등장할 확률인 $p (x$ | $θ)$ 에 비례한다.

조금 더 Likelihood에 대해 직관적으로 보기 위해 하나의 에제를 더 들어보면

획득한 데이터를 더 얻기 쉬운? 얻을 확률이 높은 곡선은 주황색 곡선이다. 이유는 곡선의 중앙 값 ( 확률이 높은값, 가능성인 높은값) 에 데이터들이 더 많이 분포했기 때문이다.

수치적으로 이 가능도를 계산하기 위해서는 각 데이터 샘플에서 후보 분포에 대한 높이(즉, Likelihood 기여도)를 계산해서 다 곱한 것을 이용할 수 있다. 곱해주는 이유는 모든 데이터들의 추출이 독립적으로 연달아 일어나는 사건이기 때문이다.

표본집합의 결합확률밀도 함수를 likelihood function이라고 하는데 위 그림과 같다.

위 식의 결과 갑싱 가장 커지는 $θ$ 를 추정값 $\hat{θ}$ 로 보는 것이 가장 그럴듯하다.

최대우도추정(Maximum Likelihood Estimation)

Likelihood(우도) 즉 식의 θ값을 최대화하는 값을 찾는 방식이 최대우도추정이다.

Maximum Likelihood Estimation(MLE)는 Random variable의 parameter를 estimate하는 방법 중 하나인데, 오직 주어진 Observation, 혹은 데이터들 만을 토대로 parameter estimation을 하는 방법이다.

참고로, 만약 observation이 i.i.d. (independent and identical distributed)하다면, $f (X | θ) = \prod_{i} f (x_{i} | θ)$ 가 되며, 여기에 log를 씌우면 덧셈 꼴이 된다. log는 단조증가함수이므로, log를 취했을 때 최대값을 가지는 지점과 원래 최대값을 가지는 지점이 동일하고, 보통 곱셈보다 덧셈이 계산이 더 간편하므로, 많은 경우에 likelihood가 아니라 log likelihood를 사용해 parameter estimation을 계산한다

MLE는 가장 간단한 parameter estimation method이지만, observation에 따라 그 값이 너무 민감하게 변한다는 단점을 가지고 있다.

예시로 모양이 일그러진 동전을 생각해보자.

모양이 일그러져서 앞이 나올 확률이 0.5라고 말할 수가 없고, 실제로 던져봐야 그 확률을 알 수 있을 것 같다. 이게 위에서 말한 가능도를 사용할 수 있는 경우이다. 경험적으로 observation한 값으로 일어날 가능성을 매기는 것이다.

실제로 1000번을 던져봤더니 앞이 400번, 뒤가 600번 나왔다면 우리는 동전을 던져 앞이 나올 확률 $p$ 가 대략 얼마 정도라고 생각할까? 아마 대부분은 0.4정도라고 생각할 것이며 이것은 $p$ 의 MLE값과 일치한다.

풀어서 설명하면 동전을 1000번 던져서 앞이 400번 나올 가능성을 최대로 하는 $p$ 는 0.4라는 뜻이며 수식을 이용한 엄밀한 증명은 다음과 같다.

위 증명은 이해가 안되는 부분이 있어서 더 찾아보고 공부할 생각이다.

확률p에 대한 가능도 L의 값을 그래프로 그리면 다음과 같다.

동전을 1000번 던져 앞이 400번, 뒤가 600번 나왔다면 우리는 직관적으로 앞이 나올 확률 $p$ 는 0.4 정도라고 생각할 것이며, 실제 이런 일이 발생할 가능성을 최대로 하는 $p$ 를 계산하면 0.4가 된다. 이를 간략히 $p$ 의 MLE는 0.4라고 표현한다.

마지막으로 조금 수학적인 얘기로 MLE를 생각해보면 어떤 함수의 최대값을 찾는 방법 중 가장 보편적인 방법은 미분계수를 이용하는 것이다. 즉, 찾고자하는 파라미터 $θ$ 에 대하여 다음과 같이 편미분하고 그 값이 0이 되도록 하는 $θ$ 를 찾는 과정을 통해 likelihood 함수를 최대화 시켜줄 수 있는 $θ$ 를 찾을 수 있다. 혹시 이 경우에서 미분이 불가능할 경우에는 그래디언트 디센트등 반복적이고 점진적인 방식으로 $θ$

편미분하는 공식은 위와 같이 생각하면 된다.

마지막으로 정리를 하자면

특정 상황에 따라 확률을 구할때 공식적으로 복잡한 경우가 있다. 이번 정리에서는 개념적인 부분과 이를 바탕으로 직관적으로 Likelihood와 MLE를 이해하는 것이 목표다.

최대우도추정 기법으로 추정한 모수(θ)는 일치성(consistency)과 효율성(efficiency)이라는 좋은 특성을 가지고 있다고 한다. 일치성이란 추정에 사용하는 표본의 크기가 커질 수록 진짜 모수값에 수렴하는 특성을 가리킨다. 효율성이란 일치성 등에서 같은 추정량 가운데서도 분산이 작은 특성을 나타낸다.

최대우도추정은 관측치(표본)에 큰 영향을 받기 때문에 이를 보완하는 다양한 기법이 제안되었다.

Reference

- rpubs.com/Statdoc/204928

- angeloyeo.github.io/2020/07/17/MLE.html
저작자표시 변경금지

'확률 및 통게' 카테고리의 다른 글

정보 이론 개념 Study (0) 2022.05.17
관련글 관련글 더보기
- 정보 이론 개념 Study
댓글