2장. 벡터 공간 I

우리가 앞에서 배운 소거법은 Ax = b 에 대한 한 종류의 이해만을 알려준다. 우리의 주요한 목표는 이와 다른 더 깊은 이해를 얻는 것이다.

 

벡터공간

벡터 공간(vector space)의 개념을 알아보자.

 

공간 Rn은 성분이 n개인 열 벡터 전체로 이루어진다. 예를 들어 n이 2이면 통상적으로 x,y 평면 2차원으로 표현한다. 

 

모든 벡터 공간 안에서 다음의 두가지 연산이 가능하다.

 

1. 임의의 두 벡터를 더할 수 있고, 모든 벡터에 스칼라를 곱할 수 있다.

2. 바꿔 말하면, 일차 결합을 취할 수 있다.

 

즉 선형결합(Linear Combination) 연산이 같은 공간상에 존재하는 벡터들 사이에 가능해야 한다.

 

정의 : 벡터 공간의 부분 공간은 벡터 공간의 요구 조건들을 만족시키는 비지 않은 부분 모음이다. 곧, 다음과 같이 일차 결합은 부분 공간에 속한다.

( i ) 부분 공간의 임의의 두 벡터 x와 y의 합 x+y는 그 부분 공간에 속한다.

( ii ) 부분 공간의 임의의 벡터 x와 임의의 스칼라 c의 곱 cx는 그 부분 공간에 속한다.

다시 말해 부분 공간은 덧셈과 스칼라 곱셈에 관해 '닫혀 있는 부분 모음' 이다.

 

특히 영 벡터는 모든 부분 공간에 속한다.

 

가장 작은 부분 공간 Z는 단 한개의 벡터인 영 벡터만을 포함한다. 이것은 '영차원 공간'인데, 원점만을 포함한다.

이것이 가장 작은 벡터 공간이다.

 

행렬 A의 열공간(column space)은 A의 열들의 모든 일차 결합을 포함한다.

연립 일차 방정식 Ax = b 를 풀 수 있기 위한 필요 충분 조건은 벡터 b를 A의 열들의 일차 결합으로 표현 할 수 있는 경우이다. 이 때 b는 열 공간에 속한다.

 

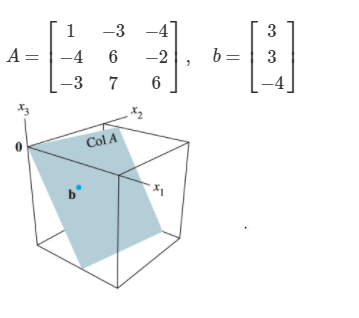
위 그림에서 행렬 A의 열공간은 파랑색 부분이다. 열 벡터 사이의 선형 결합을 통해 다른 열 벡터를 만들 수 있다. 따라서 열 공간이 그림 처럼 2차원 평면이 되는 이유다. 

 

행렬 A의 퇴화 공간은 Ax= 0인 벡터 x 전체로 이루어진다. 이를 N(A)로 나타낸다. 열 공간이 Rm의 부분 공간이듯이, 이것은 Rn의 부분 공간이다.

 

---

선형 독립과 선형 종속

 

c1v1 + ··· + ckvk = 0 은 c1 = ··· = ck = 0일 때만 나타난다고 하자. 그러면 벡터들 v1, ···, vk는 선형 독립(linear independence)이다. 0이 아닌 c들이 있으면, v(벡터)들은 선형 종속(linear dependent)이다. 한 벡터는 나머지 벡터들의 일차 결합이다. 

 

공간적으로 생각해보자. 같은 직선에 놓인 두 벡터는 종속적이다. 같은 평면에 놓인 세 벡터는 종속적이다. 특별히 우연한 경우가 아니라면, 임의로 선택한 세 벡터는 (한 평면에 있지 않고) 선형 독립이다. 

 

그림을 예를 들어 생각해보자.

2차원 벡터 v1,v2의 관계는 Linear dependent이다. v2는 v1의 두배(스칼라곱)에 해당하는 길이를 가지고 있기 때문이다. 

즉 2v1-v2 = 0이다. c1 = 2, c2 = 1 일때의 선형 조합을 통해 0이 만들어지기 때문에 두 벡터는 종속 관계이다.

직관적인 관점으로 생각해보면 벡터의 크기는 바뀌어도 되지만 방향이 바뀌면 종속 관계는 성립하지 않는다.

 

위의 두 벡터는 Linear independence 이다. 두 벡터 v1와 v2를 어떠한 선형 조합을 해도 0을 만들 수 없다. (c1,c2가 0인 경우는 제외) 이를 직관적으로 보면 두 벡터를 통해 2차원 공간에서 어떠한 벡터도 만들 수 있기 때문에 둘은 독립 관계이다.

이러한 3가지 경우는 무엇일까?

위의 정의에서 설명안했는데 위와 같은 벡터를 행렬 A의 colum으로 생각하면 A는 m * n 행렬 즉 2 *3 행렬이다. 열이 너무 많아서 일차 독립일 수가 없다. 즉 n > m이면 Rm에 속한 n개의 벡터는 일차 종속이다. 

 

---

Span

 

Span의 사전적 의미는 동사로써 (많은, 넓은 것을) 포괄하다, 걸치다, 가로지르다 등이 있다.

 

span은 보통 span a space라고 표현한다. 즉 어떤 공간을 포괄하는 것이라고 생각하면 될 듯 싶다. 선형 조합(Linear combination)을 통해 만들어지는 공간을 의미한다. 

 

정리하자면

벡터 v1, v2, ··· vn 들의 가능한 모든 선형 조합(Linear combination)으로 공간을 형성하는 것을 의미한다. 이때 공간은 조Rn이 될 수도, 혹은 부분 공간(subspace)이 될 수도 있다.

 

벡터들의 모든 가능한 선형 결합(Linear combination)에 대한 결과 벡터들을 하나의 공간에 넣은 것을 의미한다. 벡터에 따라서 모든 공간을 채울 수도, 2차원에서는 line, 3차원 공간에서 평면과 같이 부분적인 공간만을 채울 수도 있다.

---

기저(basis)

 

벡터 공간 V의 기저(basis)는 다음 두 성질을 만족시키는 일련의 벡터들이다.

 

1. 이 벡터들은 일차 독립이다.

2. 이 벡터들은 V를 생성한다.

 

즉 기저벡터들은 공간을 span 한다고 할 수 있다. 어떤 행렬 A의 column space를 생각해보자. column vector들을 선형 조합(Linear combination) 하여 column space를 만든다. 이 때 column vector들은 독립일 수도, 종속일 수도 있다. 

 

여기서 벡터들은 어떤 공간을 span 하면서 그들이 독립인 벡터들이다. 이 벡터들이 기저다.

 

3차원 공간 R3을 생각해보자. R3에 대한 기저는? 

가장 기본적인 기저벡터는 아래 그림과 같다. 

 

v1, v2, v3 세 벡터를 이용하면 3차원 공간 전체를 span 할 수 있다. 이 colum 벡터를 행렬로 만들면 단위행렬이다. 단위행렬의 Null space는 오직 [0,0,0] 인 zero vector이다.

 

3차원 공간의 기저는 무수히 많다. 

만약 여기서 column 벡터가 2개만 있으면 이는 독립이래도 기저 벡터가 아니다. 어떤 평면(plane) 만을 'span' 할 수 있기 때문이다. 여기서 7번의 식은 1번째와 2번째를 합치면 3번째 벡터가 된다. 즉 독립이 아니므로 기저가 아니다.

 

첫번째 벡터와 두번째 벡터가 이루는 평면에 3번째 벡터가 포함 될 것이다. 3차원 공간 전체를 span 하지 않는다.

 

8번 식은 독립을 만족하면서 3차원 column 벡터로 이루어져 있으므로 공간 전체를 span하고 R3의 기저라고 할 수 있다.

---

차원(dimension)

 

벡터 공간에는 기저가 무수히 많을 수 있지만, 모든 기저에 공통점이 있다. 기저 벡터의 개수는 공간 자체의 속성이다.

벡터 공간 V에 대한 임의의 두 기저에는 같은 개수의 벡터가 포함된다. 모든 기저에 공통인 이 수가 V의 차원(dimension)인데, 그 공간의 '자유의 정도'를 표현한다.

기저는 일차 독립인 최대 모음이다 더 커지면 일차 독립일 수 없다. 기저는 또한 공간을 생성하는 최소 모음이다. 더 작게하면 공간을 생성할 수 없다. 

 

예를 들어 R6 에 속한 첫째와 마지가 성분이 0인 벡터들의 모음이 있다. 4차원 부분 공간의 원소는 (0,5,1,3,4,0)과 같이 6차원 벡터이다. 

위 그림은 3차원 공간의 부분 공간인 2차원 평면에 대한 기저이다. 

R3의 벡터가 위와 같다고 할때 기저에 대한 조건 자체는 충족한다. 독립적이고 선형 결합을 통해 형성할 수 있는 공간을 span 한다. 하지만 R3의 기저는 아니라는 것이다.  

 

여기서 Rank 라는 개념을 알고 가자. 책에는 안나와 있어서 따로 찾아 보았다. 

 

계수 (Rank)의 정의

- 선형대수에서 어떤 행렬 A의 열계수(column rank)는 선형 독립인 column 벡터의 최대 개수이다. 마찬가지로 행계수(row rank)는 선형 독립인 행 벡터의 최대 개수이다.

 

행렬에서 열개수와 행계수는 항상 같으며, 이를 계수 정리라고 한다.

어떤 행렬 A의 Rank는 행렬 A의 column space C(A)의 차원(Dimension)이다.

 

Rank(A) = number of pivot columns = Dimension of C(A)

행렬이 주어지면 가우시안 소거법을 이용해 행사다리꼴 형태로 바꾸어 준다. pivot 이라 할 수 있는 0이 아닌 행을 가지는 개수를 rank A 라고 할 수 있다. 위 그림은 colum이 아니고 행을 기준으로 했다.

---

Null Space

 

Null Space의 정의이다.

 

선형 방정식 Ax = b 에서 b가 zero vector(=Null vector, = 0 벡터) 일때 식을 만족시키는 모든 가능한 해 x에 대한 집합이다. 선형방정식 Ax =0의 해들이 이루는 공간이 Null Space를 의미한다.

3차원 공간에서 Null space는 공간 R3의 부분공간이다. 기하학적으로 생각하면 직선의 형태로 표현된다. 

 

참고자료 : Learn Again! 러너게인 twlab.tistory.com/