[CS231n] 6강 Training Neural Networks I
앞 시간에 CNN, SGD 등을 배웠다. 설명은 생략하겠다.

6강,7강이 Training Neural Network이다. 이번시간에는 Activation Functions(활성화 함수) 와 Data Preprocessing(데이터 전처리)에 대해 배운다.
Activation Functions

데이터 입력이 들어오면 가중치 W와 곱한다. 그리소 활성화함수 비선형연산을 걸친다.
즉 Activation Function은 f=wx에 대해서 input이 들어오면 이 값을 다음 노드로 보낼때 값을 어떻게 보낼지를 정해주는 함수이다. 보통 non-linear 함수를 사용한다.
활성화 함수의 역할은 말 그대로 '활성화'를 시켜주는 것이다. 함수의 종류에 따라 형태도 다양하다.

이제 이 함수들에 대해 하나하나 알아보자.

먼저 sigmoid 함수이다. 3가지의 문제점도 한꺼번에 가져왔다.
단순한 단일,이진 분류에서 많이 사용한다. 하지만 최종 출력에만 사용하고 중간에 사용하지 않는다.
그 이유가 3problems 으로 나와 있다.
1. Saturated neurons "kill" the gradients
가장 큰 문제인 gradients vanishing 이다.
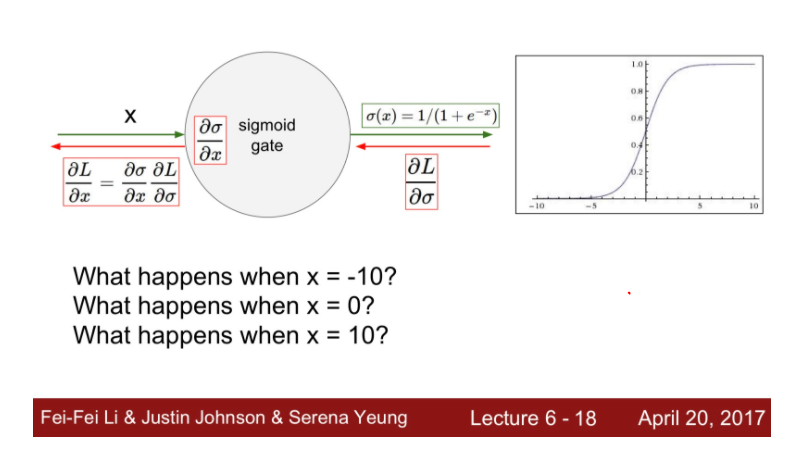
시그모이드 함수 그래프를 보자. x가 -10,0,10 이면 값이 어떻게 되는가??
-10일때의 기울기는 거의 0이다. 10일때도 마찬가지이다. 그나마 0일때의 기울기가 0.5정도면
(1-0.5)*0.5 = 1/4 근데 이걸 backpropagation을 하면 점점 기울기가 소실된다.
2. sigmoid의 출력이 zero-centered가 되어 있지 않다.

시그모이드 그래프를 보면 0을 중심으로 되어있지 않다. 이게 뭐가 문제가 될까???
x가 모두 양수라고 하자. 가중치와 곱해지고 활성화함수를 통과하면 언제나 양수가 된다.
이 상태에서 W의 gradient의 값은 시그모이드 함수를 미분하면 된다. Local gradient를 계산하면 그냥 X이다.
부호는 위에서 내려온 gradient의 부호와 같다.

즉 음수면 음수 양수면 양수의 gradient값을 가진다.
파라미터를 업데이트하면 모두 증가하거나 감소할 것이다. 이상적인 그래프는 대각선으로 가야 하는데
지그재그로 가면서 비효율적임을 알 수 있다. 2차원적으로 생각해보면 사분면 즉 영역을 2개만 사용하므로 마찬가지로 비효율적이다.
3. sigmoid의 exp 연산의 값이 매우 어려운 연산이다.
계산량이 오래걸린다. 그래서 sigmoid는 잘 쓰이지 않는다.

다음 함수는 tanh(x) 이다. zero centered가 되었다. 하지만 아직 gradient vanishing와 exp 연산 문제가 해결되지 않았다.

다음은 ReLU 함수이다. 가장 대중적으로 사용하는 activation function이다.
간단히 0이하는 0으로 하고 0이상은 그 값을 그대로 내보낸다. 그래서 f(x) = max(0,x) 라는 식을 가진다.
매우 단순하면서 잘 작동하는 활성화함수이다.
하지만 이것도 문제가 있다.
일단 0이하 값들은 다 버리게 된다. 그리고 zero centered도 되어 있지 않다.

x 값이 -10이랑 0일 경우 gradient가 0이 되게 된다.
만약 이렇게 되면 "dead ReLU" 에 빠진다.

위에 보이는 Data Cloud에서 멀어지면 activate가 일어나지 않고 값이 update 되지 않는다. activate Relu는
일부만 update 된다.
초기화를 잘못할 경우 가중치 평면이 Data Cloud와 멀리 떨어져 있는 경우다. 이런 경우 어떤 데이터도 update 안되고 backpropagation도 일어나지 않는다.
learning rate가 높을 경우 update를 지나치게 크게 해서 가중치가 날뛰면 Relu가 데이터 영역을 벗어난다.
그래서 결론적으로 update시 relu를 활성화 될 가능성을 조금이라도 높여주기 위해 아주 작은 positive biasese를 추가한다. 결과는 반반이라고 한다.
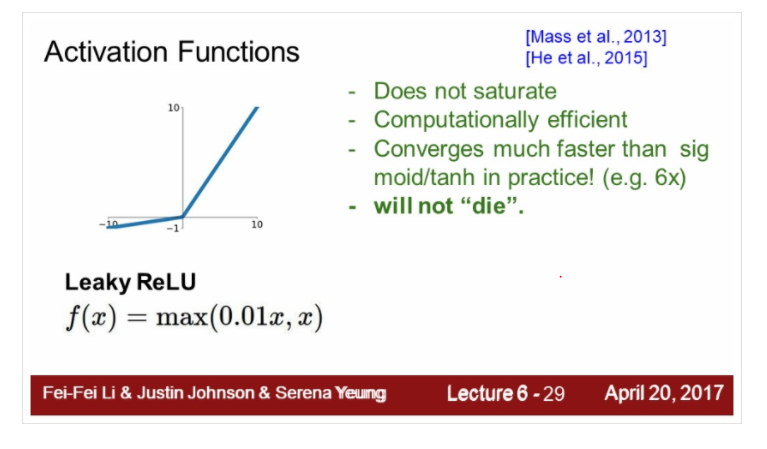
Leaky ReLU이다. 0이하의 값들을 0.01값을 줘서 작은 값이라도 주게 하는 것이다.
will not "die"

조금 변형한게 PReLU이다. 알파값을 줘서 backprop을 해서 일종의 학습을 통해 찾아가는 그런 개념이다.
saturation을 막고 Dead ReLU도 나타나지 않는다.

ELU다. ReLU의 모든 장점을 가지고 있고 zero mean 형태를 띈다.
saturation이 잡음에 강인할 수 있다고 한다.
아직 exp 계산을 해야하는 단점은 존재한다.

Maxout Neuron이다. 잘 사용하지 않는데 max 값을 통해 2개의 파라미터를 주고 그 중에 더 좋은 것을 선택하는것인데
문제는 계산량이 2배로 늘어난다는 단점이 있다.

일반적으로 RelU를 사용하고 tanh는 LSTM에서 자주 사용한다.
시그모이드는 사용하지 않는다.
Data Preprocessing

다음은 데이터 전처리이다.
대표적인 전처리는 zero-centered 와 normalized 이다.
normalized는 특점 범위내에 데이터 값을 모아두는 것을 말한다. 데이터간의 차이가 크면 값의 폭이
너무 크니까 그래프가 이쁘게 나오지 않는다. 표준편차로 나눠주면 되는데 이미지 처리에서는 이미 0~255라는 픽셀값이 정해져있으니까 굳이 하지 않고 zero-centered를 한다. 차원간의 스케일이 어느 정도 맞춰져있다.
그외에도 분산에 따라 차원을 축소해주는 PCA나 whitened data 등이 있다.
Weight Initialization

다음은 가중치 초기화다. 만약 가중치가 0이라면 어떻게 될까?
모두 다 같은 연산을 수행한다. 출력도 같고 gradient도 같다. 뉴런이 똑같이 생기게 된다.
첫번째 방법은 랜덤의 작은 값을 넣는 것이다.

생각보다 잘되지만 network가 깊어질수록 문제가 된다.
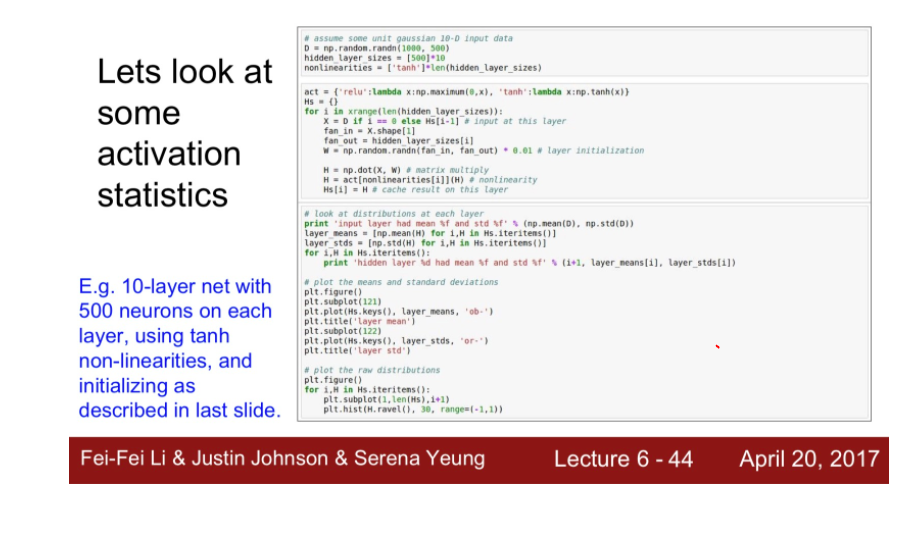

10개의 layer로 구성된 네트워크이고 레이어당 500개의 뉴런이 존재한다 활성화 함수는 tanh로 잡았다.
layer가 깊어질수록 값이 다 날라간다.
분포를 보면 가우시안(표준정규분포) 형태로 나타나있다. 하지만 W를 곱할수록 W가 작은 값이라 출력 값이 점점 줄어들고 0으로 향한다. 모든 활성화 함수 값들이 0이 될 것이다.

반대로 W의 값을 크게 잡으면 오버슈트가 일어나고 -1 ~ 1에 saturated 된다.

좋은 weight 값을 주기 위해 xavier initialization을 사용한다.
노드의 개수를 normalized하자는 것이다. 큰 값은 큰걸로, 작은 값은 작은걸로 나눠준다.
입/출력의 분산을 맞춰주는 역할을 한다.

하지만 ReLU 같이 non-linearity에서는 적용되지 않는다.

그래서 2015년 he 초기값이 나온다. 추가적으로 2를 나눠주는 방식을 사용한다. relu에서 2를 나눠준다.
ReLU에서 출력의 절반을 죽이기 때문에 출력의 분산을 조정해준다.
작은 변화가 매우 큰 차이를 보인다. 하지만 Batch Normalization을 하면 굳이 weight initalization을 안해줘도 된다.
Batch Normalization

BN은 내가 따로 논문을 읽어서 정리해 놓은 관계로 간단히 설명하겠다.
activation을 gaussian하는것이 아니라 BN은 학습하는 과정 전체를 , 즉 모든 layer 가 Unit gassuain이 되게 한다.
internal covariance shift를 방지하기 위해 각층의 input 분포를 평균0 표준편차1인 분포로 만들어 준다.

Batch당 N개의 학습 데이터가 있고 데이터가 D차원이라면 각 차원별로 평균을 구해준다. 그리고 Batch 내에서 normalize를 한다.

FC나 Conv layer 뒤에 사용한다. activation 전에 잘 분포되도록 해준다고 생각하면 된다.

최근에 논문에서 본 식이다. mini-batch mean을 구하고 variane (분포)를 구하고 normalize 한다.
scale은 어느 정도 값이 퍼지게 하는지를 정하고 shift는 이동성이다. 이 두 값은 학습을 통해 구한다.
보통 BN을 쓰면 Dropout을 쓸 필요가 없다고 한다.
위의 초록색 글씨로 BN의 효과를 알 수 있다.
Babysitting the Learning Process
1. Data preprocessing
2. Choose the architecture
3. loss is reasonable
4. training
5. training with regularization and learning rate

먼저 처음은 데이터 전처리이다. 보통 이미지 인식에는 zero-centered 를 한다.

그 다음 이제 architecture를 선택한다. hidden layer는 어떻게 구성할지, 대충 사이즈를 잡아놓고 생각한다.
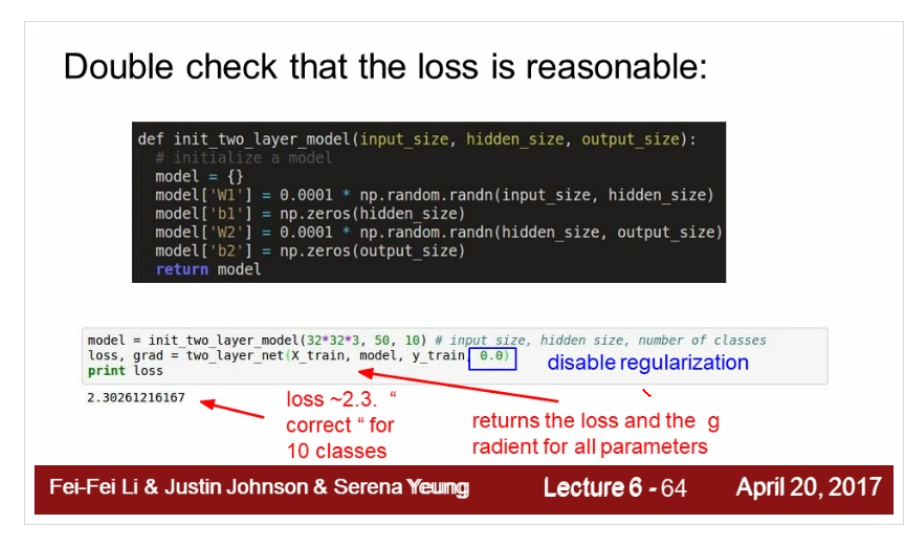
loss 값이 잘나오는지 합리적인지 확인을 한다.
우리의 layer가 동작하는지 확인하는 것이 앞에서 말한 sanity check 이다.

그 다음 training 한다. 작은 데이터 셋을 먼저 넣는다.
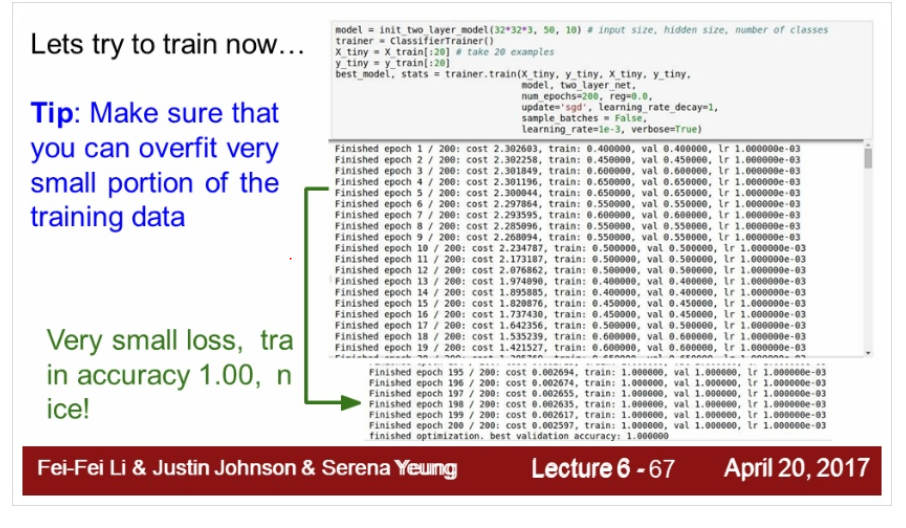
데이터의 값이 너무 작으면 당연히 오버피팅이 일어난다.

이제 regularization 값과 learning rate 값을 찾아본다. 적절한 값을 넣어서 찾아본다.
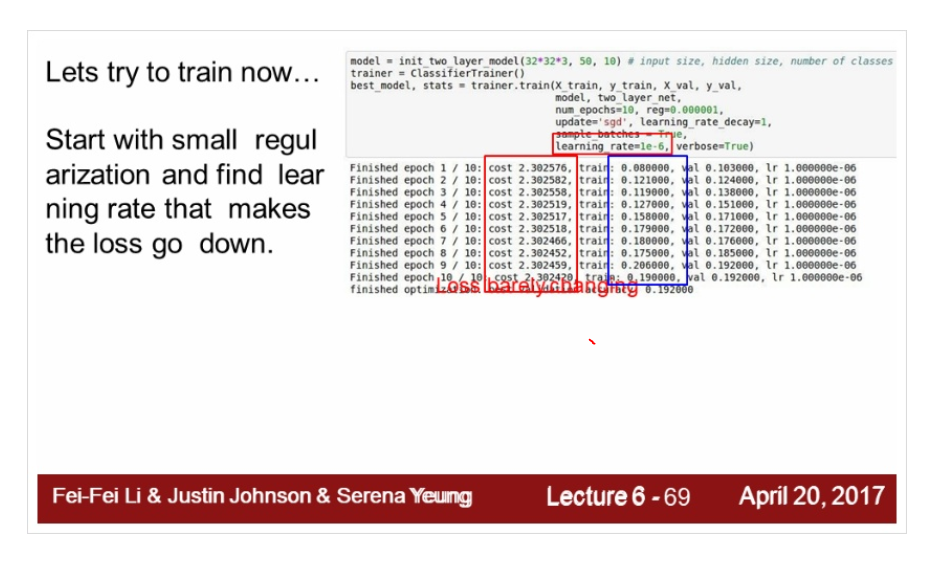


train, accuracy 값이 변화하는 것을 보면서 learning rate를 조절한다.
Hyperparameter Optimization

넓은 범위에서 좁은 범위로 줄여나가며 값을 찾는다.
Cross-validation 전략 : training set으로 학습시키고 validation set으로 평가한다.
log 값을 취해주면 더 안정적인 값을 얻을 수 있다.

Random Search는 말 그대로 랜덤으로 찾는거고
Grid Search는 하이퍼파라미터를 고정된 값과 간격으로 샘플링한다.
일반적으로 랜덤으로 하는 것이 더 좋은 값 영역에 접근할 확률이 좋다고 한다. 보통 둘 중 random search를 사용한다.

Loss가 발산하면 learning가 높은것이고 너무 평평하면 너무 낮은 것이다. 그래프를 보면 알 수 있다.
good learning rate는 비교적 가파르면서 지속적으로 일정하게 내려가는게 좋다.

이런 Loss도 보인다. 이건 초기화 문제이다. 적절한 값을 못찾아서 훈련이 되지 않다가 어느 순간 갑자기 지점에 다달아서 한번에 확습이 되는 것이다. Gradient의 backpropagation을 생각하면 된다.

Training accuracy 와 validation accuracy이 차이가 많이나면 overfitting을 의심해야 한다.
이 경우 regularization의 강도를 높여야 할 수도 있다.
gap 이 적다면 아직 capacity을 높일 여유가 있다는 것이다.
overfitting은 항상 유의해야 하는 부분이다.
가중치의 업데이트 되는 정도 또한 중요하다. 한번에 업데이트가 너무 크게되거나 적게되면 안된다.

마지막으로 여태까지 주제에 관한 중요한 Summary다.
이상으로 6장을 마치고 7강에서는 나머지 부분을 배운다.