2장. 그래프와 네트워크
선형 대수의 응용에 대한 내용이다. 물체 인식을 위한 카메라 캘리브레이션, 물세 자세 추정을 위해 세그멘테이션된 바이너리 이미지의 Eigenvalue 및 Eigenvector 등의 사용, 또한 각종 머신 러닝등을 사용할 때에도 선형대수를 이용한다.
이번 절에서는 그 중에 그래프와 네트워크에 관련된 내용이다. 두가지 장점을 지닌 한 부류의 직사각 행렬들을 도입한다. 이런 직사각 행렬은 단순하고, 중요하다.
이것은 그래프의 결합 행렬(incidence matrix of graph)인데, 모든 성분이 1 또는 -1 또는 0이다. 놀라운 점은 L과 U 및 네가지 부분 공간 모두의 기저 벡터에 대해서도 이것이 참이라는 사실이다.
Graph
우리가 생각하는 그래프는 2차원 평면에 있는 단순한 그래프 일 수도 있다. 하지만 이산수학에서의 그래프는 어떤 네트워크 형태의 구조를 의미한다. 그래프(graph)는 꼭지점(vertex) 또는 마디(node)의 모음과 꼭짓점들을 연결하는 변 또는 모서리(edge)의 모음으로 이루어진다. 그래프의 화살표가 존재하면 이것을 유향(directed)이라고 한다.

유향 그래프 그림이다. 오른쪽 그림을 행렬로 표현해 적용하면 된다.
그래프는 응용수학(Applied mathmatics)에서 가장 중요한 모델 중 하나이며, 이산(discrete)적 형태를 띄고 있다.
에지(edge)는 각 노드들을 연결시켜주는 역할을 한다.
Incidence Matrix
그래프의 노드와 edge간의 연결관계를 행렬(Matrix)로 나타낼 수 있다. 이러한 그래프를 근접행렬(Incidence Matrix)라고 부른다.

위와 같은 그래프가 있다고 하자. node의 개수를 n, edge의 개수를 m이라고 할 때 n = 4, m = 5가 된다. n을 행렬의 column, m을 row로 하여 5*4 근접 행렬을 만들 수 잇다. 이 그래프의 edge는 방향성을 가지고 있는 유향성을 띄고 있으므로 방향성을 표시해줘야 한다. edge1의 경우 node1에서 출발하여 node2로 간다. node1이 출발점 = -1, node2가 도착점 = 1로 설정한다.

위와 같은 근접행렬을 만들 수 있다. 근접행렬을 알면 그래프를 그릴 수 있을 것이다.
node들이 연결되어 있는 부분 그래프(subgraph)를 Loop라고 한다. 행렬을 보며 따라가도 되지만 그림으로 Loop를 찾는방법은 도형의 부분 면적 개수를 찾으면 된다. 위 그림에서는 edge1,2,3 이렇게 1개, edge3,4,5 1개, edge 1,2,4,5 이렇게 1개 총 3개의 Loop가 있다.
이 Loop를 고려해서 행렬을 생각해보자. edge 1,2,3은 서로 Loop 관계이다. 여기서 이 row들이 독립인가?
이 말은 즉슨 행렬 A의 loop에 해당하는 row들은 서로 독립이낙를 묻는 것이다. edge1 * -1 + edge 3 = edge2이다. 독립 관계가 아니고 종속 관계이다.
여기서 알 수 있는 점은 어떤 그래프의 loop애 대한 incident matrix의 row들은 선형종속(linearly dependent)의 특성을 갖는다는 점이다.
책에서는 네 가지 기본적인 부분 공간이 각각 그래프에서 의미를 지니고 그 의미를 설명한다.
A의 퇴화 공간 (Null Space)
Ax = 0 이 되는 열들의 일차 결합이 있는가? 답은 소거를 통해 얻지만 여기서는 한눈에 알 수 있다. 열들을 더하면 영 열이 된다.
위 행렬로 계속 예를 들어보자. 책에서는 n1,n2,n3,n4를 꼭짓점에서의 전위(전압)로 생각한다. Ax의 다섯 성분은 다섯 모서리를 통한 전위 차를 알려준다. edge1 을 통한 전위차는 첫째 행의 n2-n1이다.
모든 전위를 똑같은 상수 c만 큼 올리거나 내릴 수 있고, 전위 차는 바뀌지 않는다. x = (c,c,c,c)가 A의 퇴화 공간에 속함을 확인해준다. 이런 벡터들만이 퇴화 공간에 속하는데, Ax = 0 은 모든 모서리를 통해 전위가 같음을 뜻한다. 이 결합 행렬의 퇴화 공간은 일차원이다. 계수는 4- 1 = 3이다.

하나의 예를 들어 생각해보자.
A의 null space를 구한다는건 node를 나타내는 column이 독립인지를 파악할 수 있다. Ax = 0을 풀면 되지만 그래프 적으로, 전자회로처럼 생각해보자. node들을 전자 회로에서 전압을 측정하는 임의의 지점이라고 생각해보자. Incidence matrix와 연관 지어 변수 x = (x1,x2,x3,x4)들은 각 node에서의 전압이다. 이때 행려 A의 전압을 곱하면 우리는 각 node들의 전위차(potential difference)를 계산 할 수 있다.

위 Incidence matrix를 전자회로적 관점으로 다음 그림 처럼 생각 할 수 있다. 이제 우리가 찾는 것은 node들의 전위차가 0이 되는지다. null space를 찾는 것이니까. 물론 모든 x가 0인 경우에는 전위차가 0이다. 근데 여기서 0은 전위차가 없다는건데 이는 회로에서 전류가 흐르지 않는 것이기 때문에 의미가 없다. 위 column 은 모두 더하면 0이 된다. 즉 column vector는 dependent 한다는 것이고 영 벡터 이외의 해가 존재한다. x가 1일 경우 해가 된다.
x가 1로만 이루어진 벡터는 결국 node의 가능성이 constant 하다는 것을 의미한다. node의 전압이 constant 하다면 node들의 전위차는 0이고 이것은 Ax = 0 인 null space의 해이다. Null space는 Ax =0 의 해의 공간을 의미한다.
x는 해의 집합을 가지고 어떤 1차원의 line으로 존재한다. 위에서 얘기한 x = (c,c,c,c) 처럼 이 형태의 값이 존재하고 null space의 기저(basis)는 x = (1,1,1,1) 이다.
모든 노드의 전압을 올리거나 내릴 수 있는 파라미터가 단 한개만 존재하는 것이다.
위와 같은 경우는 회로에서 의미가 없다고 했다. 그래서 전위차를 만들어 주기 위해 node들 중 하나를 grounnd로 설정하고 나머지를 풀 수 있다. 회로적인 개념으로 생각해보면 쉽다. 어떤 한 column을 0으로 만들고 나머지 x값들을 푸는 것이다. ground는 전압이 0이 되는 것이고 기준 전압이 된다는 것이다. 이렇게 전위차를 만들고 전류의 흐름을 만든다.
여기서 위에서 말했듯이 Incidence matrix의 Rank(계수)가 4-1 = 3 이기 때문에 ground는 1개만 하고 나머지 3개의 node를 가지고 해를 구한다.
열공간
위에서 말한 선형독립, 종속을 생각해보자. 위에서 edge1 - edge3 + edge2 = 0, edge5 - edge4 + edge3 = 0 을 볼 수 있다. 다섯 성분에 대한 두 가지 조건이 있는데, 열 공간의 차원이 5 - 2 이기 때문이다. 이런 조건들은 소거를 통해 얻을 수 있다.
여기서 그래프의 의미로 고리라는 개념이 나온다.
고리 : 키르히호프의 전압 법칙에 따라, 한 고리( 루프, loop)에서의 전위차를 더하면 영이다.
위에서 말한 loop에 대한 개념이다. loop에 해당하는 edge를 더하면 0이 된다.
| 어떤 전위차 b1, ..., b5에 대해 Ax = b 를 풀때 b가 열 공간에 속하기 위한 판정법은 다음과 같은 키르히호프의 전압 법칙이다. 한 고리(Loop)에서의 전위 차의 합은 반드시 0이다. |
왼 퇴화 공간(left nullspace)
행렬 A의 left nullspace는 N(A(t:전치행렬) 표기에서 알 수 있듰이 At(전치행렬)의 nullspace이다.
At(전치행렬) * x =0 을 만족시키는 x들의 집합이 A의 left nullspace이다.
이제 이 식을 풀기 위해 그래프에서 의미를 찾자. 벡터 y 의 성분은 다섯 개인데, 각각 한 모서리에 대응한다. 이런 수들은 다섯 개의 모서리를 따라 흐르는 전류를 나타낸다.

Null space of a transpose는 키르히호프의 전류 법칙과 관련이 있다.

위 행렬을 이렇게 나타내 보자. row1이 의미하는 것은 node1이다.
그럼 첫번째 행은 node1에서 edge1,3,4로 전류가 나간 것을 의미한다. node1에서 흘러나간 전류의 총 합은 0이다.
row2를 보면 y1=y2 이다. node2에 들어온 전류는 y1, node2에서 흘러나간 전류는 y2이다. 다음 행을 봐도 똑같이 알 수 있다. 들어온만큼 나간다 라는 키르히호프의 전류의 법칙을 설명해주는 평형방정식(balance equation)이다.
차원을 생각해보자. dim N(At(전치행렬))을 알기 위해선 행렬에 대한 3가지 성분을 알아야 한다.
column , row, rank 이다. 왼 퇴화 공간에 차원은 m-r이다. 여기서 m = 5 (열), r = 3(계수) 이다.
사실 m-r 은 행렬에서 소거했을때 free column으로 나타나는 부분들이다. 이 개수가 결국 차원의 개수가 된다. 그럼 이 공간의 기저는 무엇일까?
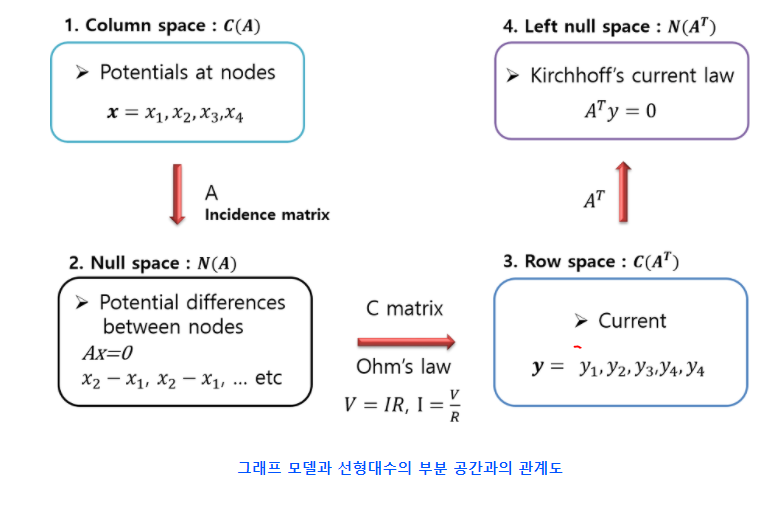
그래프 모델과 선형대수의 부분 공간의 관계를 이해하기 아주 좋은 그림이다. 책만으로는 이해가 부족해 Learn Again1 러너게인 님의 블로그를 정말 많이 참고했다.
4개의 주요 부분 공간(four fundamental subspaces)이 전자회로의 그래프 모델에서 찾고자 하는 것과 매우 연관이 있따. 이 부분 공간을 잘 이해하는 것이 중요하다. 그래서 이 내용을 따로 정리 할 예정이다.
Left null space의 해를 구하는 과정은 전치하고 소거를 통해 pivot과 free variable을 구하면 특별해를 구할 수 있고 null space를 알 수 있다. 하지만 키르히호프의 전류 법칙을 이용해 Loop 단위로 node들 사이에 edge로 표현 된 전류의 흐름을 따져서 기저를 구하는 방법이 가능하다.

차원이 2이므로 기저는 두개의 special solution이어야 한다. Loop1을 보자. y1을 1로 정하면 y2도 1이다. node1에서 출발한 전류가 node2를 거쳐 node3으로 흘러가기 때문이다. 아니면 식을 보면 y1-y2 = 0 으로 되어 있다. 여기서도 y1 = y2를 알 수 있다.
y3 = -1이다. node1에서 1만큼의 전류가 나갔다. 나간만큼 들어와야 한다. node3 입장에서는 y3은 들어오는 전류이다. 그러므로 1이 아닌 -1로 설정해준다. loop1을 기준으로 기저를 찾고 있으므로 나머지 y4,y5는 0으로 만들어 준다. 그러면 해가 나왔다. 첫번째 해는 y = [1,1,-1,0,0] 이다. 이 해를 가지고 row1,2,3,4를 계산하면 특이해가 맞는 것을 확인 할 수 있다. 두번째 기저 또한 같은 방법으로 구하면 [0.0.1,-1,1] 이다.
node1,2,3,4 로 된 큰 Loop를 이용해 해를 구하면 [1,1,0,-1,1]이라는 해가 나온다. 이 해는 기저로 포함할 수 있을까??
아니다. 왜냐하면 이 해는 앞에서 말한 두 special solution의 합이므로 dependent하다고 할 수 있다. 기저는 독립적이어야 하기 때문에 이 해는 기저로 사용 할 수 없다.
행 공간
A의 행 공간은 모든 벡터를 포함하지는 않는다. 차원은 계수 3이다. 일차 독립인 행들은 대응하는 모서리가 Loop를 형성하지 않는다.

A transpose의 column space인 row space(행 공간)를 살펴 보자. 앞서 rank = 3 이라는 것을 알았다. 이 뜻은 소거법을 사용해서 행렬을 정리하면 pivot column이 3개이고 free column이 2개라는 말이다. 위의 Incidence Matrix를 보면 column1,2,4가 독립(independent)인것을 확인 할 수 있다. col1,2,3은 서로 dependent하다.
서로 independent한 이들 pivot column에 해당하는 edge들만 표시하고 연결하면 원래 있던 Loop가 없어진다고 한다. 이렇게 Loop가 없는 형태의 그래프를 우리는 TREE라고 부른다.
이러한 성분은 행 공간에 대한 기저이다. 행 공간은 퇴화 공간에 수직이다. f가 행 공간에 속하고 x가 퇴화 공간에 속하면, fT(전치행렬)x = 0 이다.
모든 그래프들에 대해서 node와 edge, 그리고 loop의 관계에 대해서 정리하자면 다음과 같다.
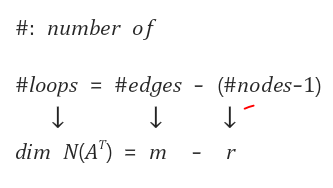
여기서 nodes - 1 은 rank(계수)를 의미한다. 그래프의 Incidence matrix에서 항상 rank = n-1이기 때문이다.
n은 column의 개수이고 1개의 column은 종속이므로 빼주면 rank가 된다.
edge의 수는 row의 수와 같고 노드의 수는 column의 수와 같다. 독립적인 loop의 개수는 그래프의 Incidence matrix의 left null space와 같다.
4가지 부분 공간에 대한 개념이 부족해서 이해하는데 힘들었다. 따로 이 부분을 정리해야겠다.
참고자료
- Learn Again! 러너게인 twlab.tistory.com/29
- MIT Linear Algebra (Gilbert Strang) www.youtube.com/watch?v=6-wh6yvk6uc